Introduction
Attention is a mechanism in transformers (a central part of most commonly-used LLMs) that assigns varying importance to different input tokens, enabling the model to focus on relevant parts of the input when making predictions. It is inherently sparse because most tokens primarily attend to a few key elements.
Over long contexts, the computation required for attention balloons rapidly because of its O(N^2) time complexity where N is the number of tokens. However, its sparsity can be leveraged to reduce the amount of computation required and speed up prefill (when the model is processing the prompt, before it starts generating text) significantly while producing results that are nearly equivalent to performing full attention. Taking advantage of this sparsity is important for developing fast and efficient solutions to problems that use a long context window.
Interesting Papers
MInference
MInference, released by Microsoft last summer, worked towards reducing the time for prefill by 10x on a million-token prompt. MInference tested out 3 approaches:
- Block-sparse attention: block selection was performed by averaging the keys and values in a giving block together (as performed in the "averaging" method below)
- A-shape attention: as attention is generally focused on the starting tokens, compute attention using the first n tokens and the most recent m tokens for each block. This is the approach described in StreamingLLM.
- Vertical-slash attention: the best-performing approach, this method relies on finding the right configuration for a pattern with diagonal blocks in a slash pattern and some global vertical tokens. This approach is training-free, but with some slight tuning to find the configuration that would work best for the given model.
SeerAttention
SeerAttention trains a linear layer in each attention head to produce a transformed version of the pooled query and key weights over a block. These pooled queries and keys then have RoPE embeddings added to them before a coarse attention map is generated. Because the reference for this would normally be a map derived from a fully computed attention map, computing the loss traditionally would be prohibitively expensive over a long context. To mitigate this, the authors write a custom Triton kernel to produce the reference block-scale attention map from performing max pooling over each block.
Exploring further
An important part of block-sparse attention is finding which blocks should be attended to. This is usually done by performing a pooling operation over consecutive chunks of k tokens in the key and value matrices and then producing an attention map over these pooled matrices. Since the block size is substantial (64, 128, etc.), it is much quicker and far less expensive than having to compute a full attention map.
Most of what I've seen with block-sparse attention uses a pooling step that averages the keys/values in a given block across the hidden dimension. However, are there any other approaches to pooling that may yield better stronger results?
How do you actually evaluate the quality of the pooling method?
I went through 3 different approaches for comparing the attention weights in a coarse attention map to the ones that would be generated by fully computing attention.
My initial thought was to calculate the block weights and then compute the KL divergence between the target distribution (which would be computed from the actual attention weights), and the generated distribution (which would be computed from whichever technique was being used to compute the blocks that needed to be attended to). Testing this out, however, I was dealing with large divergence values in some cases that made it challenging to interpret the results.
My next idea was to compute the attention fully using the QKV matrices without block sparse approaches and then compare it to various methods of selecting blocks for block sparsity. This would be efficient in terms of memory usage because FlashAttention could be used, and it would avoid computing the O(N^2) intermediate attention map matrix. However, doing this would require computing different attention outputs for varying levels of sparsity.
It turns out that you don't need the full attention map to figure out which blocks are the most important - you need a mapping from each token to each block or from each block to the other blocks. Then, after calculating the most important blocks from the matrix multiplication after the pooling, the weight of each relevant block can be added one at a time to account for how much of the attention weight for each token had been accounted for. Finally, these values can be averaged across the heads and the number of examples.
Another consideration was regarding how to treat the blocks being processed at the edge of the causal mask. Since it can be generally assumed that, when computing block-sparse attention, the blocks on the edge of the grid will automatically be computed as part of a sliding window, I decided to mask out the blocks on the edge and recompute based on the other blocks.
Pooling approaches
In this blog post, I tested out the following approaches:
- Averaging - this is the regular method, where you average across the dimensions for each block
- Softmax Averaged - for each token, softmax is performed over the head dimension before averaging
- Max-min - take the maximum value across the dimensions for each block and concatenate with the minimum value across the dimensions for each block (this doubles the head dimension size for when the important blocks are calculated).
- Chunked max min, then averaging - for each block, for subchunks of varying sizes, find the maximum and minimum values for that chunk. Then, average the maximum and minimum values across the number of subchunks in a given block.
- Chunked averaging, the max and min - same as above, but within each subchunk, average over the hidden dimension before taking the minimum and maximum across the hidden dimension for each chunk.
For the chunked approaches, my goal was to find some way to combine the max-min and averaged pooling approaches. This approach took inspiration from triangular range searching algorithms that solve up to a certain depth with one method and then beyond that depth with a different method.
Evaluating and results
I evaluated these approaches using prompts from LongBench-v2. The maximum length for prompts I used was 32000, and I chose the first 100 prompts from the "long" subset of the benchmark. The model I chose for this was Llama-3.2-1B because of its small size and large context length.
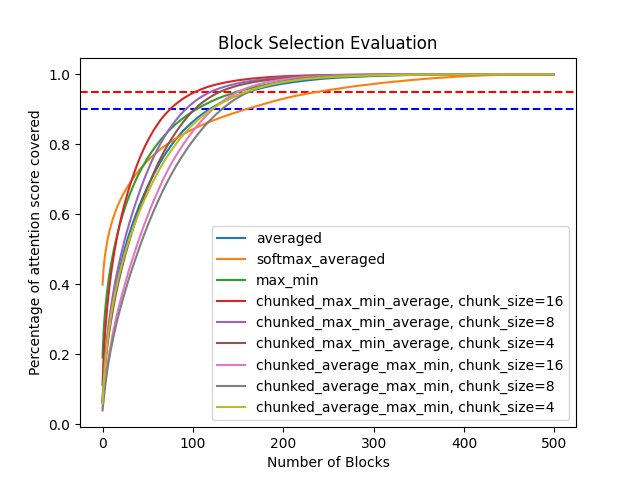
Overall, the results show there can be more optimal pooling methods than just averaging over the whole block:
Graphed Results
Table

Summary
From the graph and table above, it seems that mixing averaging across a whole block and selecting by the minimum and maximum values for specific chunks provides a more effective way of building a coarse attention map.
Next Steps
For some next steps,
- It might be good to switch to a different evaluation metric, such as InfiniteBench.
- Analyze the effect of padding tokens in some examples. Although I tried minimizing the amount of padding used and keeping prompts uniform by truncating the document, this might introduce an unwanted bias towards one of the methods.
Code
Feel free to explore the repository to see how each method was implemented, and please let me know if there are any improvements that I should make or errors to fix.